
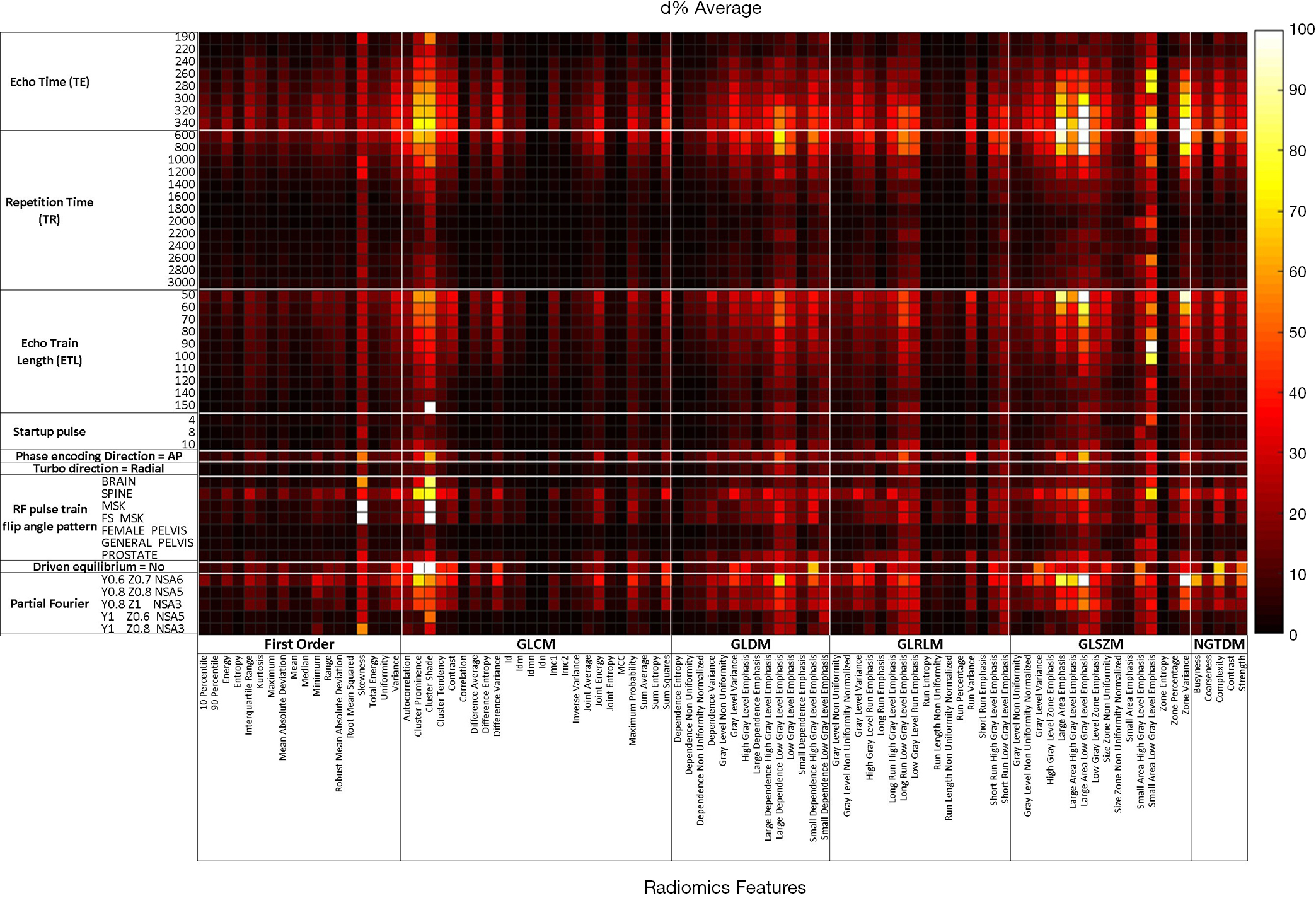
For instance, they are foundational in the modern scientific understanding of sound, heat, diffusion, electrostatics, electrodynamics, thermodynamics, fluid dynamics, elasticity, general relativity, and quantum mechanics ( Schrödinger equation, Pauli equation, etc). Partial differential equations are ubiquitous in mathematically oriented scientific fields, such as physics and engineering. Among the many open questions are the existence and smoothness of solutions to the Navier–Stokes equations, named as one of the Millennium Prize Problems in 2000. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. The function is often thought of as an "unknown" to be solved for, similarly to how x is thought of as an unknown number to be solved for in an algebraic equation like x 2 − 3 x + 2 = 0. In mathematics, a partial differential equation ( PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function.
A visualisation of a solution to the two-dimensional heat equation with temperature represented by the vertical direction and color.


 0 kommentar(er)
0 kommentar(er)
